Nicolas ERDRICH
Page en construction
15/01/2023
« Il est impossible de bien combiner deux choses sans une troisième : il faut entre elles un lien qui les assemble. Il n'est pas de meilleur lien que celui qui de lui-même et des choses qu'il unit fait un seul et même tout. Or, telle est la nature de la proportion. » Platon, Timée
Certains auteurs ont étudié les rapports de proportion que l'on peut trouver entre les longueurs des différentes parties d'un animal ou d'un végétal.
En plaçant trois points distincts \(\text{A}\), \(\text{B}\) et \(\text{C}\), et en désignant par \(a=\text{BC}\), \(b=\text{AC}\) et \(c=\text{AB}\) les distances entre ces trois points, on peut définir six rapports de longueurs, \(\frac{a}{b}\), \(\frac{b}{c}\) et \(\frac{c}{a}\) et leurs trois inverses respectifs \(\frac{b}{a}\), \(\frac{c}{b}\) et \(\frac{a}{c}\).
Lorsque le rapport est tel que \(\dfrac{a}{b}=\dfrac{a+b}{a}\), on appelle Nombre d'Or la valeur du quotient \(\dfrac{a}{b}\), nombre noté \(\Phi\), solution positive de l'équation \(x^2-x-1=0\) égale à 1,61803398875...
Le nombre d'or, égal à \(\dfrac{1+\sqrt{5}}{2}\) est un rapport de proportions bien connu, utilisé, de manière consciente ou non, par de nombreux artistes et artisants pour produire des œuvres ou des objets harmonieux.
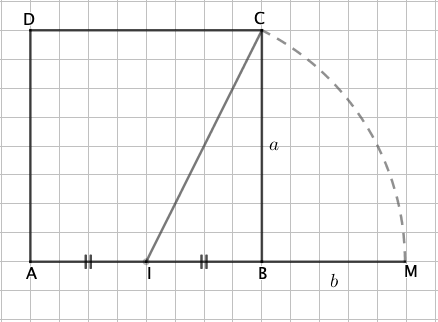
Lorsque le rapport de deux segment est égal au nombre d'Or, on parle de section dorée. Sur la figure ci-dessous, on a illustré une manière simple d'obtenir une construction géométrique d'une section dorée. ABCD est un carré de coté de longueur \(a\) et I est le milieu du segment [AB]. En notant \(b=\text{BM}\) où M est le point d'intersection du cercle de centre I et de rayon IC avec la demi-droite [IB), il vient que \(\dfrac{a}{b}=\dfrac{a+b}{a}\).
Johannes Kepler (1571-1630) est sans doute le premier savant à avoir constaté la présence de la section dorée dans les rapports de proportions des parties des végétaux. Kepler indiqua la correspondance entre la divine proportion et la suite de Fibonacci où chaque nombre s’obtient par la somme des deux précédents. Kepler, fasciné par le Nombre d’Or, écrivit que « la géométrie contient deux grands trésors : l’un est le théorème de Pythagore, l’autre est la division d’une ligne en moyenne et extrême raison ; le premier peut être comparé à une règle d’or, le second à un joyau précieux» .




