Qu'est-ce qu'une lunule ?
On appelle lunule une surface concave-convexe délimitée par deux arcs de cercles sécants de rayons différents. Une lunule ressemble à un croissant de Lune, d'où son nom.
Représentation de lunules
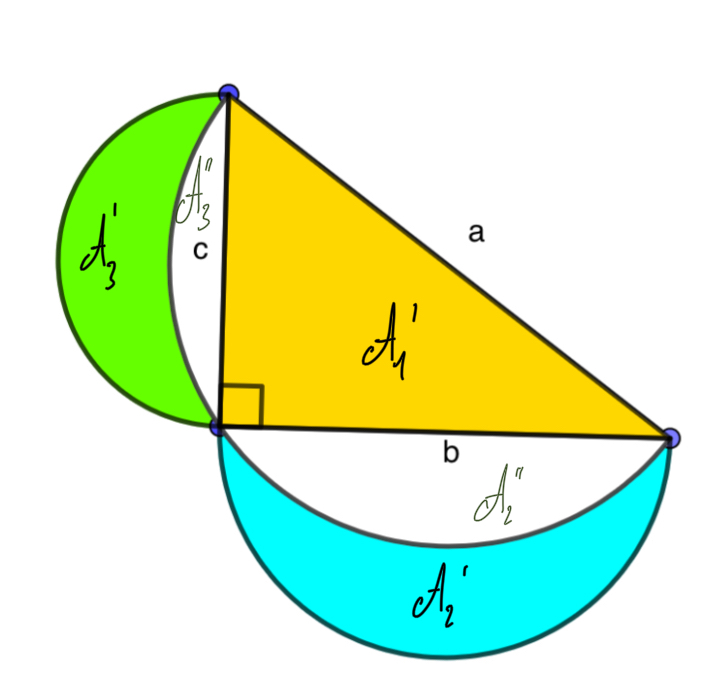
Les lunules d'Hippocrate de Chios sont des surfaces définies à partir de demi-cercles construits sur les côtés d'un triangle rectangle comme représenté ci-dessous :

Hippocrate de Chios
Hippocrate (-470 à -410) est un mathématicien grec originaire de l'île de Chios. On sait de lui uniquement ce que quelques successeurs, dont Aristote et Proclus, en ont rapporté. Précédant Euclide d'un siècle, il est l'auteur d'une somme (Éléments) résumant les mathématiques de son époque. Le premier histoirien des sciences, Eudème de Rhodes (-370 à -300), en rapporte un long fragment dans ses propres écrits.
On sait en particulier qu'Hippocrate s'intéressa à deux problèmes géométriques. Le premier problème est celui de la duplication du cube. Il consiste à déterminer comment construire un cube de volume double d'un cube donné. Le second problème est celui la quadrature. Il consiste à construire à la règle et au compas un carré dont l'aire est identique à celle d'une figure donnée. Pour ce qui est de la quadrature de lunules, Hippocrate est à l'origine d'un théorème concernant les lunules construites sur les côtés d'un triangle rectangle isocèle.
Théorème d'Hippocrate
Théorème d'Hippocrate : la somme des aires des lunules verte et bleue est égale à l'aire du triangle jaune.

Conséquence directe :
La somme des aires des lunules construite sur les côtés d'un carré est égale à l'aire du carré.
Preuve du théorème d'Hippocrate
Remarquons que nous pouvons étendre ce théorème à tous les triangles rectangles (et pas seulement aux triangles rectangles isocèles).
Considérons d'abord les aires \(A_1, A_2\) et \(A_3\) des demi-cercles construits sur les côtés du triangle rectangle.
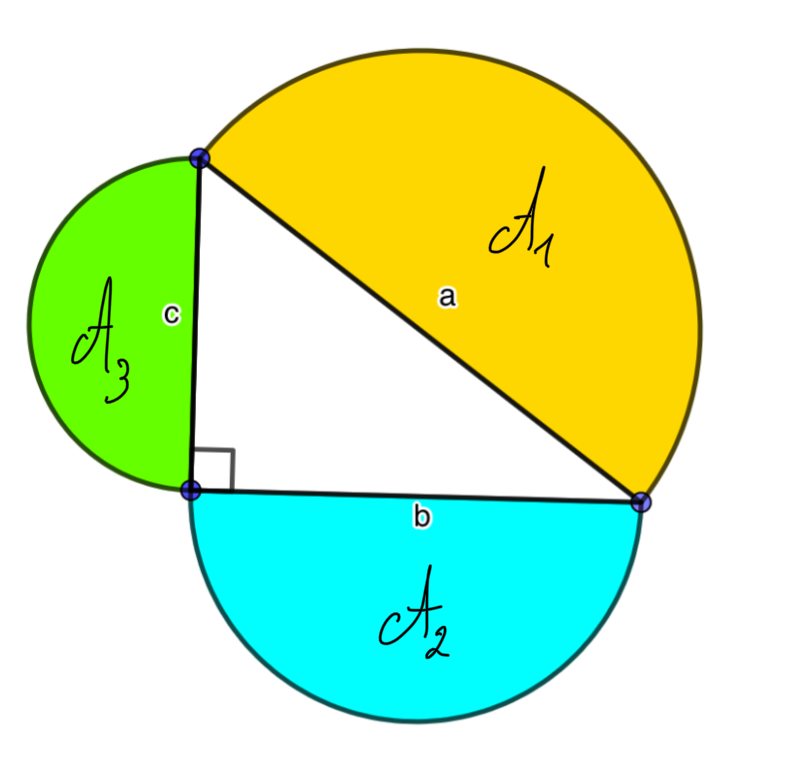
1) Montrons que \( A_2 + A_3 = A_1\)
1re méthode (par calcul direct des aires) :
\[A_2 = \dfrac{1}{2} \times \pi \times \Big(\dfrac{b}{2}\Big)^2 = \dfrac{\pi}{8} b^2\]
de même,
\[A_3 = \dfrac{1}{2} \times \pi \times \Big(\dfrac{c}{2}\Big)^2 = \dfrac{\pi}{8} c^2\]
donc :
\[A_2 + A_3 = \dfrac{\pi}{8} (b^2+c^2)\]
\[= \dfrac{\pi}{8} a^2 \ \ \ \text{(par le théorème de Pythagore)} \]
\[= \dfrac{1}{2} \times \pi \times \Big(\dfrac{a}{2}\Big)^2 =A_1\]
2e méthode (plus générale, à l'aide d'agrandissements) :
Comme les demi-cercles construits respectivement sur les côtés \(b\) et \(c\) sont des réductions de rapports \(\frac{c}{a}\) et \(\frac{b}{a}\) du demi-cercle construit sur le côté \(a\), il vient que :
\[A_2+A_3 \]
\[= \Big(\dfrac{c}{a}\Big)^2 \times A_1 + \Big(\dfrac{b}{a}\Big)^2 \times A_1\]
\[=\dfrac{b^2+c^2}{a^2} \times A_1\]
\[=\dfrac{a^2}{a^2} \times A_1 \text{ (par le théorème de Pythagore)}\]
\[=A_1\].
Corollaire : remarquons au passage que cette démonstration permet de généraliser le théorème de Pythagore à n'importe quel triplet de surfaces semblables construites sur les côtés d'un triangle rectangle. Sur la figure ci-dessous, l'aire de la figure jaune est égale à la somme des aires des figures bleue et verte.

2) Montrons maintenant que \(A'_2 + A'_3 = A'_1\).
D'après ce qui précède, on a :
\[A'_2 + A''_2 + A'_3 + A''_3 = A_1 \]
En outre, par symétrie d'axe le côté de longueur \(a\), on a aussi :
\[ A_1 = A'_1 + A''_2 + A''_3\]
Ainsi,
\[A'_2 + A''_2 + A'_3 + A''_3 = A'_1 + A''_2 + A''_3\]
en simplifiant cette expression, on aboutit à :
\[A'_2 + A'_3 = A'_1\]
Cqdf.