Nicolas ERDRICH
17/12/2022
Dire que Jean et Marie regardent la même photographie peut se dire en deux sens : soit qu'ils regardent tous les deux une seule et même photographie, soit qu'ils regardent, chacun de son côté, des photographies similaires. Dans le premier cas, le terme de "même" renvoie à une identité numérique : il n'y a qu'une seule photographie. Dans le second cas, on parle d'indiscernabilité : il y a deux photographies très ressemblantes.
En logique, il existe un principe appelé "indiscernabilité des identiques" (en abrégé, Inid). Ce principe affirme que, si a est numériquement identique à b, alors a et b partagent toutes leurs propriétés. Le plus souvent, on utilise ce principe sous sa forme contraposée : s'il existe la moindre différence entre a et b, alors on peut en déduire que a est numériquement distinct de b. Ce principe semble plutôt intuitif, et somme toute, assez solide, mais il existe cependant des philosophes, comme Peter Geach, qui l'ont contesté [1].
Quoi qu'il en soit, il ne faut pas confondre le principe d'indiscernabilité des identiques avec sa converse, appelée "identité des indiscernables" (Idin). Celle-ci affirme que si a et b partagent l'intégralité de leurs propriétés, alors a est identique à b. Dans sa version contraposée, ce principe consiste à affirmer que, pour tout couple d'individus, il existe toujours une propriété qui les différencie, autrement dit, une propriété possédée par l'un mais pas par l'autre.
Comme on le voit, l'identité des indiscernables rabat la ressemblance parfaite sur l'identité numérique. Le principe Idin fait beaucoup plus polémique que le principe Inid. De fait, nous pouvons nous demander s'il existe ou s'il pourrait exister des choses parfaitement indiscernables, quoique numériquement distinctes. Le philosophe et mathématicien allemand Gottfried Wilhelm Leibniz (1646-1716) est célèbre pour avoir nié cette possibilité :
« Il n'y a rien de tel que deux individus indiscernables l'un de l'autre. Un gentilhomme ingénieux de ma connaissance, s'entretenant avec moi en présence de Son Altesse Électorale la Princesse Sophie, dans le jardin de Herrenhausen, crut trouver deux feuilles parfaitement semblables. La princesse le défia de le faire, et il courut longtemps dans tout le jardin pour en chercher ; mais c'était inutile. » [2]
\Avant d'aller plus loin, remarquons que l'indiscernabilité peut se dire pour signifier, là encore, des choses différentes. On peut vouloir dire que ces choses partagent toutes leurs qualités, comme leur taille, forme, leur couleur, leur matière, etc. Par exemple, dans Alice au pays des merveilles de Lewis Carroll (1832-1898), les personnages de Tweedledum et Tweedledee sont qualitativement indiscernables : ils ont la même allure, ils sont revêtus de manière similaire, bref, ils sont en tous points ressemblants. En revanche, outre leur distinction onomastique, il y a bien au moins une façon dont Tweedledum et Tweedledee diffèrent : par le fait d'occuper synchroniquement des emplacements différents. Par exemple, l'un est à la droite d'Alice, quand l'autre est à sa gauche. Même parfaitement ressemblants par leurs qualités respectives, ils restent relationnellement discernables. Ils ne partagent pas leurs propriétés spatiales. Ainsi, des choses peuvent être discernables soit par leurs qualités soit par leurs relations. Lorsque deux individus partagent, comme Tweedledum et Tweedledee, l'intégralité de leurs qualités sans toutefois partager leurs propriétés relationnelles, on appelle répliques pures [3] de tels doubles.
\Les symboles et les signes sont généralement utilisés de telle manière que leurs occurrences soient indiscernables les unes des autres. Ils sont conçus pour apparaître comme des types picturaux de répliques pures. Par exemple, les deux lettres « a » du mot « mathématiques » sont des images qualitativement indiscernables. Ceci est justifié par le fait que ces deux occurrences doivent être substituables sans que la signification du terme en souffre.
C'est également le cas pour les deux panneaux « sens interdit » de circulation routière représentés ci-dessous, qui se donnent comme des images qualitativement indiscernables.
Dans certains cas, l'orientation de l'image permet d'en différencier la signification. En logique, la première lettre majuscule de l'alphabet est employée à l'envers (« ∀ ») pour désigner le quantificateur universel. Les deux occurrences, ayant même forme, même taille, etc. sont qualitativement indiscernables, mais en revanche elles sont relationnellement distinctes pour le lecteur, l'une étant pivoté de 180 degrés par rapport à l'autre. Cette différence relationnelle est employée pour évoquer une distinction sémantique.
C'est aussi le cas des deux panneaux ci-dessous où le premier astreint à une obligation de céder le passage alors que le second signale un danger. Notons toutefois que vus de dos, ces panneaux sont généralement mal différenciés par les conducteurs : c'est sans doute moins l'orientation que le signe dessiné dessus qui permet de les identifier correctement.
Certaines images représentées sur des objets de la vie quotidienne sont conçues non seulement comme des répliques pures, mais également pour être perçues de façon indiscernable selon des angles de vue distincts. Dans de tels cas, la symétrie centrale s'avère alors extrêmement utile. Par exemple, sur la carte à jouer ci-dessous, en déplaçant le curseur rouge, on peut constater que l'illustration est symétrique par rapport au centre du rectangle : le motif est vu de la même façon par deux joueurs situés face à face. Chaque joueur peut ainsi reconnaître directement la carte quelle que soit son orientation par rapport à elle.
Mais considérons maintenant les exemples suivants : les deux images ci-dessous donnent pour impressions de représenter à gauche une bosse et à droite un creux. Or en déplaçant le curseur rouge pour effectuer une rotation d'un demi-tour de l'image de gauche, on constatera que celle-ci est qualitativement indiscernable de celle de droite. Quoique ces deux images soient des répliques pures, nous ne les comprenons pas de la même façon. Selon l'angle sous lequel nous les percevons, celles-ci sont interprétées comme relevant d'objets convexes (en relief) ou concaves (en creux).
On peut constater le même phénomène sur les photographies suivantes.
Ci-dessous, la même photographie d'un bol a été pivotée de 180 degrés. L'image de gauche (l'originale) représente l'intérieur d'un bol. Celle de droite semble représenter le dessous du bol.
Lorsque la figure est retournée, les objets initialement convexes sur l’image de départ apparaîssent alors concaves, et inversement, ceux qui semblaient concaves paraissent alors convexes.
Cette illusion, appelée illusion du cratère, a été étudiée par le neuroscientifique V.S.Ramachandran entre 1988 et 1990. Selon lui, nos manières de percevoir les images précédentes trahissent un principe cognitif que nous appliquons sans en avoir conscience. Le cerveau traduit la position relative des parties ombrées comme une information concernant le relief de l'objet observé, lui attribuant des propriétés qu'il ne possède pas toujours ! L'illusion produite provient du fait que l'image est interprétée en pronostiquant que la source lumineuse est unique, qu'elle est fixe et qu'elle est située au dessus de l'objet observé. Reconnaissons que dans notre environnement naturel, cette hypothèse est plutôt adéquate. Mais dans les cas où la source de lumière ne répond pas à ces trois présuppositions, elle devient erronée. Même informé de ceci, il nous est impossible de réviser cette conjecture cognitive, d'où la persistance de l'illusion.
Deux images peuvent donc être parfaitement indiscernables de manière purement qualitative tout en paraissant très différentes lorsqu'on modifie leur orientation par rapport à l'observateur. Des répliques pures peuvent donc, par le jeu de relations spatiales, se manifester comme finalement peu ressemblantes.
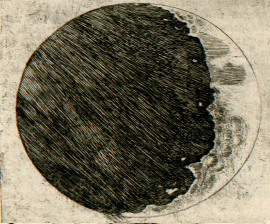
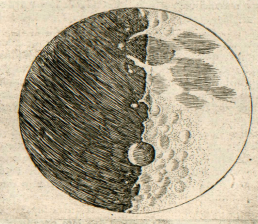
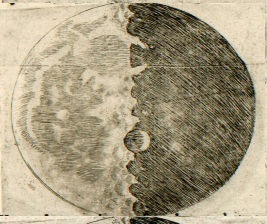
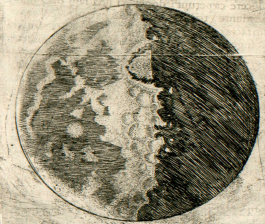
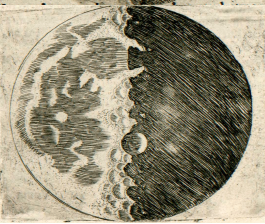
Le problème prend une tournure remarquablement importante lorsqu'il s'agit d'interpréter des photographies d'objets pour lesquels nos perceptions sont limitées, par exemple lorsqu'ils sont hors d'atteinte du toucher. Une même photographie du sol lunaire peut ainsi être interprétée de manières très différentes selon l'orientation de l'image. Jugez vous-même en observant les deux illustrations ci-dessous : a-t-on affaire à une montagne ou à un cratère ?
Le phénomène avait déjà été étudié en 1826 par le physicien David Brewster (1781-1868), qui est aussi connu pour être l'inventeur du Kaléidoscope.
Brewster avait notamment étudié différents phénomènes optiques dont celui de la polarisation de la lumière. Il a découvert ce qui est aujourd'hui appelé « angle de Brewster » ou encore « angle de polarisation ». Il s'agit d'un angle d'incidence selon lequel la lumière, avec une polarisation particulière, est parfaitement transmise à travers une surface diélectrique transparente, sans réflexion. Lorsque la lumière non polarisée est incidente à cet angle, la lumière qui est réfléchie par la surface est donc parfaitement polarisée.
Mais l'analyse des ombres sur la surface de la Lune est plus ancienne encore. Galilée (1564-1642) avait déjà utilisé les propriétés des ombres pour déterminer, grace à la lunette astronomique de son invention, le relief du satellite de la Terre. Il affirme que ce dernier est tout en creux et en bosses. C'est contraire à la conception lisse qui prédominait alors, dont la tradition remontait à Platon, qui considérait les astres comme des sphères parfaites. Galilée constate, au gré de ses observations de la Lune, que certaines parties sombres progressent dans la lumière. D'autres, lumineuses progressent dans l'ombre. En outre, certains endroits sont éclairés avant les autres : Galilée en déduit qu'il s'agit de montagnes.
Voici ce qu'en dit précisément Galilée dans Le Messager des étoiles :
En réalité, non seulement les frontières entre les ténèbres et la lumière sont, sur la Lune, visiblement inégales et sinueuses, mais — ce qui suscite un plus grand émerveillement — un très grand nombre de points brillants apparaîssent au sein de la partie ténébreuse de la Lune, entièrement séparés et détachés de l’étendue illuminée et éloignés d’elle par un intervalle qui n’est pas peu considérable. Ces points augmentent peu à peu, après quelque temps, en grandeur et en luminosité ; après deux ou trois heures, ils se joignent au reste de la partie brillante, qui s’est agrandie désormais. Entre-temps, toutefois, de plus en plus de points, qui pullulent, pour ainsi dire, de-ci, de-là, dans la partie ténébreuse s’allument, augmentent, et finalement s’unissent à la surface lumineuse, qui est encore plus étendue maintenant. La figure de la page précédente nous en montre un exemple. Or, n’est-il pas vrai que sur la Terre, avant le lever du Soleil, quand l’ombre occupe encore la plaine, les sommets des monts les plus élevés sont illuminés par les rayons solaires ? qu’après un court laps de temps, la lumière se répand, tandis que les parties médianes, plus larges, de ces mêmes monts s’illuminent ? Enfin, lorsque le Soleil est déjà levé, les illuminations des plaines et des collines ne se rejoignent-elles pas ? Mais sur la Lune, ce type de différence entre les élévations et les cavités semble dépasser de très loin l’inégalité du relief terrestre, comme nous le montrerons plus loin [4].
[1] Geach, P. Reference and Generality, Cornell University Press, 1980. "Ontological Relativity and Relative Identity" in K. Munitz, Logic and Ontology, New York University Press, 1973.
[2] Leibniz, G. W. v. & Clarke, S. (2000). G. W. Leibniz and Samuel Clarke : Correspondence. Hackett Publishing Company.
[3] Erdrich, N. , « Répliques, doubles et coïncidents purs. Trois régimes d’indiscernables » in Philosophia Scientiæ, 2020/2 (24-2), pages 29 à 52.
[4] Galilée, Le Messager des étoiles (1610), trad. de F. Hallyn, Seuil, 2009.
